摘要

目的：我们推测与呼吸机相关的肺损伤原因可能可以归结为一个单一变量：机械功。我们评估是否可以通过机械功（由压力-容积环推导）的组成部分（潮气量（TV）/驱动压力（∆Paw）、流速、呼气末正压（PEEP）和呼吸频率（RR））来计算机械功。如果是这样，就可以估计每个变量对机械功的相对作用。

方法:将运动方程的各个分量乘以容积和RR的变化量，计算出机械功:

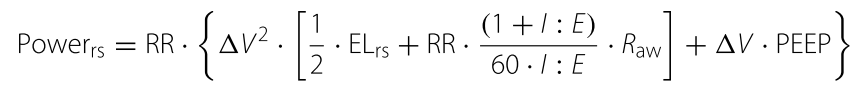
其中∆V为潮气量，ELrs为呼吸系统弹性，I:E为吸呼时间比，Raw为气道阻力。在30例正常肺患者和50例ARDS患者中，通过功率方程计算机械功，并通过5、15 cmH2O PEEP和6、8、10和12 ml/kg TV时的动态压力-容积曲线测量机械功。然后，我们计算了各个组成变量对机械功的影响。

结果:在5 cmH2O PEEP和15 cmH2O PEEP时，正常受试者和ARDS患者的计算和测量机械功相似(斜率分别为0.96,1.06,1.01,1.12,R2 > 0.96, p < 0.0001)。机械功随TV、∆Paw和流速(指数= 2)以及RR(指数= 1.4)呈指数增加，随PEEP呈线性增加。

结论:机械功方程可以帮助评估呼吸机相关原因对肺损伤的贡献及其变化。该方程可以很容易地在每个呼吸机的软件中实现。

关键词:ARDS, VILI，机械通气，呼吸力学

引言

呼吸机/通气诱导肺损伤(VILI)是由呼吸机向肺实质输送什么以及肺实质怎么接受，相互作用造成的。在过去的几十年里，我们对这两个现实的理解逐渐增加:一方面，呼吸机负荷的不同组成部分得到了不同的强调;另一方面，肺实质的条件决定了对给定的呼吸机负荷的反应已被研究和阐明。呼吸机产生VILI的原因包括压力、容积、流速和呼吸频率。另一方面，有利于VILI的肺条件主要取决于水肿量，水肿可导致肺容积减小，肺不均匀性增加，应力梯度增加，循环开放和塌陷。为了简便起见，我们在这里忽略了“肺外”因素，如灌注、pH值、气压和温度。显然，呼吸机和VILI的肺部病因可能相互作用。以呼气末正压(PEEP)为例，一方面增加呼吸机压力负荷，另一方面可能减少肺不均一性和周期性肺泡开放-闭合。然而，区分呼吸机和肺对VILI的贡献可能有助于达成更好的VILI预防策略。事实上，值得考虑的是，尽管对所有与呼吸机相关的VILI病因进行了单独调查，但它们都是独特的物理变量(即机械功)的组成部分，而大多数肺部相关VILI的病因主要是水肿量(即ARDS严重程度，至少在早期阶段)的结果。如果我们考虑机械设置，很明显潮气量、压力和流速都是能量负荷的组成部分，而能量负荷以单位时间表示就是机械功。在本文中，我们将提出一个简单的模型来量化床旁机械功，并讨论其与机械通气“安全”设置的相关性。

方法

机械功方程的推导

运动方程：根据经典运动方程(加入PEEP)，在任意时刻，整个呼吸系统的压力(P)等于:

事实上，运动方程的每个分量都是压力：

ELrs ×∆V =∆P(弹性回缩力压力分量)，即ELrs = (Pplat−PEEP)/∆V(即呼吸系统弹性)。

Raw × F = Ppeak−Pplat(运动产生的压力分量)，即Raw = (Ppeak−Pplat)/F

呼气末正压(PEEP)本身与运动无关，但它代表了肺的基线张力，因为它是∆V和流量为零时呼吸系统中存在的压力。

每次呼吸的能量

在图1中，我们表示了为了使呼吸系统的容积(∆V)大于其静息容积，必须施加给呼吸系统的能量。为了清楚起见，我们假设呼吸系统(或肺)的压力-容积曲线在考虑的容积范围内是线性的，即一直到肺总量(TLC)开始的区域。

ZEEP的每呼吸能量。能量(即充气线和y轴之间的面积)是压力绝对值(P)乘以体积变化量(∆V)，即P ×∆V。因此，当PEEP为零时，用于克服弹性阻力的能量为三角形的面积，即1/2 × Pplat ×∆V。

PEEP时每次呼吸的能量。当施加PEEP时，达到PEEP容量的能量(∆VPEEP)将等于1/2 × PEEP ×∆VPEEP，但只需要1次(只要保持PEEP)，因为在潮气量通气期间，∆VPEEP等于0，因此1/2 × P ×∆V也等于0。然而，在PEEP存在的情况下，需要更多的能量使肺充气。因此，TV达到Pplat所需的能量为∆P + PEEP(即Pplat)乘以从PEEP容积到平台压容积的位移容积。这个能量等于以Pplat和PEEP为底，TV为高度的梯形面积(见图1)。关于PEEP作用的更详细讨论，见电子补充，E-1部分。

每次呼吸气体运动的能量。这个能量几乎等于图1右侧平行四边形的面积，其中一侧是(Ppeak−Pplat)，另一侧是∆V。这种表示实际上是对现实情况的简化，因为它可能在容量控制或压力控制通气期间发生变化。

据此，我们可以用运动方程中的每个压力乘以体积变化来计算每次呼吸的能量，如下所示:

                                 (2)              

方程(2)的第一项，即∆V ×∆P，已被除以2(三角形的面积)，以近似它们的组成成分(见图1a)，而第二项和第三项不需要任何修正，因为它们代表沿轴平移。

由式(2)可知:

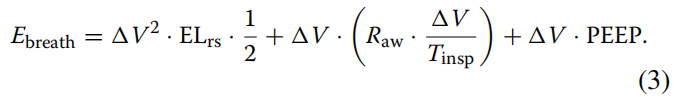
因此

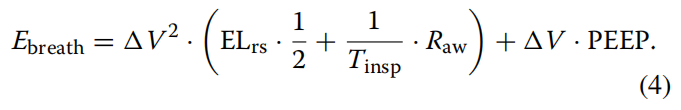
为了将Tinsp表示为呼吸速率(RR)和吸气呼气比(I:E)的函数，这两个函数在每个呼吸机设置中都很容易获得，可以应用以下推导:

前提：

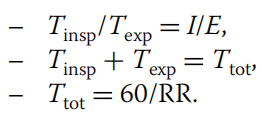
推论出：

因此，将Tinsp代入式(4):

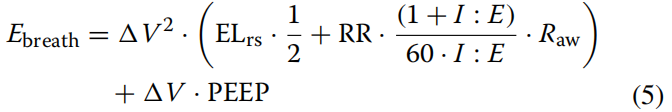
如果我们用升来表示体积，用cmH2O来表示压强，它们的乘积乘以0.098就会用焦耳来表示。

机械功

根据式(5)，机械功表示为J/min:

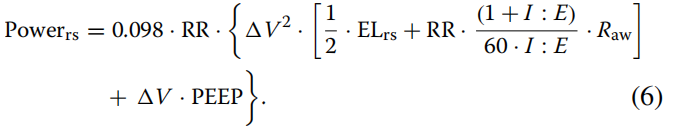
根据上述公式，可以计算改变任何变量(潮气量、驱动压、呼吸速率、阻力)对施加于呼吸系统的机械功率的影响。(6)式的简化版本以及施加在肺而不是整个呼吸系统上的机械功率的计算，见电子补充，E-2和E-3节。

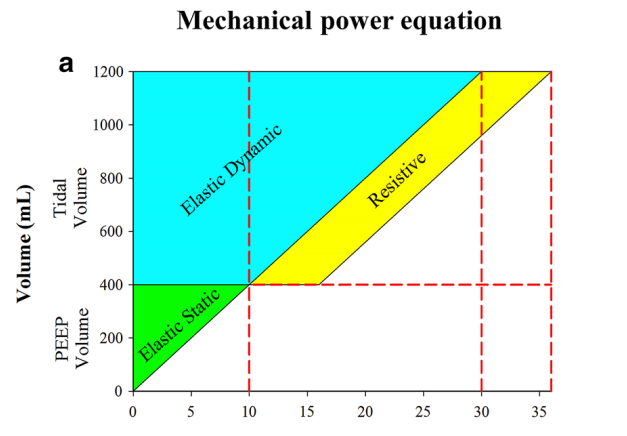
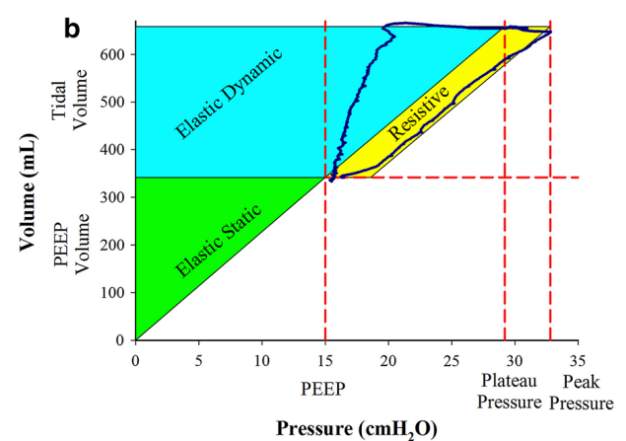
图1 a方程的图示。这个图形是由一个大三角形(绿色加天蓝色)组成的，它的右边是一个平行四边形(阻力，黄色)。大三角左侧直线代表总容积(即TV + PEEP容积)，上方直线代表平台压。斜边的斜率代表系统的顺应性(在我们的例子中1200 ml/30 cmH2O = 40 ml/cmH2O)。这个大三角形的面积是在平台压力下的总弹性能量，等于(1200 ml × 30 cmH2O)/2 × 0.000098 = 1764J。这个总弹性能量有两个组成部分:较小的三角形(静态弹性阻力，绿色)，代表PEEP应用时仅一次提供的能量，和较大的梯形(动态弹性阻力，蓝色)，其面积代表每次潮气提供的弹性能量。请注意，梯形由两个分量(都是蓝色)的和得出:一个矩形的面积是TV × PEEP(幂方程的第三个分量)，一个三角形的面积是TV ×∆Paw × 1/2，等于ELrs × TV × 1/2(幂方程的第一个分量)。功率方程的第三个分量是阻力平行四边形(黄色)所描述的面积，其面积等于(Ppeak−Pplat) × TV。b动态压力-容积环基于15 cmH2O PEEP,用下面的测量参数:Ppeak 32.8 cmH2O Pplat 29.2 cmH2O,TV 303毫升。测算能量,即梯形的面积所描述的吸气蓝线,峰值压线（平台压线？？？译者注）(长边),PEEP线(短边)和TV线(高度)是0.77 J,计算机报0.80 J . RR = 18 bpm,测量功率是13.9 J /分钟和计算机报14.4 /分钟。

施加能量/功率的测量

测量应用的能量/功率

我们使用了之前一项研究的数据，该研究包括30例肺正常的患者(19例外科和11例医学对照受试者)，其中无ARDS，以及50例ARDS患者(轻度= 26，中度= 16，重度= 8)。人群特征总结于表1(更多细节可在原始研究的表1 - 3中找到)。每例ARDS患者分别接受4种潮气量(6、8、10和12 ml/kg)和2种PEEP水平(5和15 cmH2O)。以100 Hz记录流量和气道(Paw)压力，并用专用数据采集系统(Colligo;Elekton，米兰，意大利)记录。每次呼吸所施加的能量是通过潮气通气期间记录的动态压力-容积曲线来测量的。每次呼吸提供的能量(气道+呼吸系统)定义为气道压力吸气肢与容积轴之间的面积(图1b)。注意，压力用绝对值表示(即包括PEEP)，而体积用EELV上方的容积差表示。用L× cmH2O (1L × cmH2O = 0.000098 J)表示容积-压力面积积分，用呼吸能量乘以呼吸频率得到机械功率。

统计方法

单变量logistic回归用于评估机械功率测量值和计算值之间的相关性。采用Bland-Altman分析评估机械功测量值与计算值的一致性。采用SAS 9.2软件(SAS Institute, Cary, NC, USA)进行分析。

结果

计算与测量的机械功率

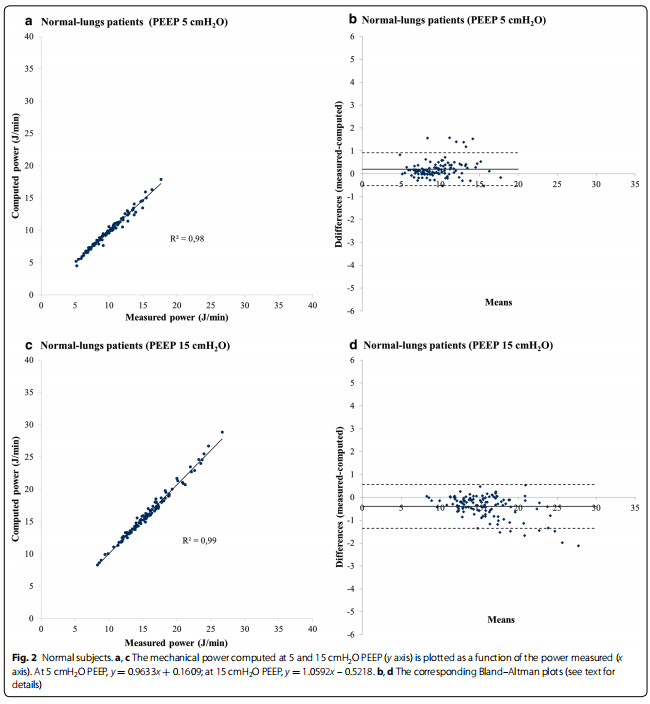
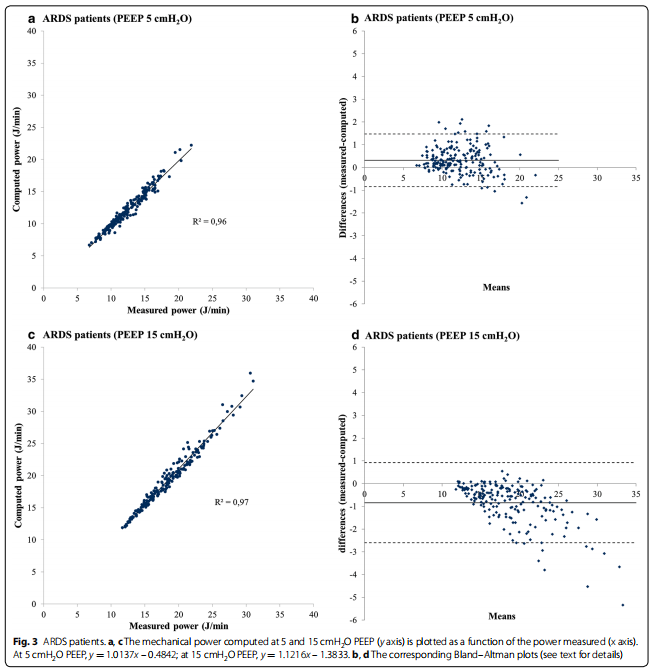
图2a (5 cmH2O PEEP)和图C (15 cmH2O PEEP)报告了在30例因与肺无关的病变(即“正常”肺)接受机械通气的患者中，测量和计算出的机械功之间的回归。分别在6、8、10、12 ml/kg TV下测量机械功率，每种PEEP水平测量120次。测量的机械功率(x轴)与通过功率方程计算机计算的机械功率严格相关，根据以下回归:计算机值= 0.96 ×测量+ 0.16,R2 = 0.98, p < 0.0001(在5 cmH2O PEEP时)和计算机值= 1.05 ×测量−0.52,R2 = 0.99, p < 0.0001(在15 cmH2O PEEP时)。相应的Bland-Altman分析见图2b, d。如图所示，在PEEP 5 cmH2O时，差异的平均值为0.196 J/min，一致性上限为0.916 J/min，一致性下限为- 0.525 J/min。PEEP为15 cmH2O时，差值均值为−0.396 J/min，一致性上限为0.560 J/min，一致性下限为−1.353 J/min。图3a (5 cmH2O PEEP)和图3c (15 cmH2O PEEP)报告了50例ARDS患者机械功测定值与计算值的回归关系。分别在6、8、10、12 ml/kg TV下测量机械功率，每种PEEP水平测量200次。测量的机械功率(x轴)与通过功率方程计算机计算的机械功率严格相关，根据以下回归:计算机值= 1.01 ×测量−0.48,R2 = 0.96, p < 0.0001(在5 cmH2O PEEP时)和计算机值= 1.12 ×测量−1.38,R2 = 0.97, p < 0.0001(在15 cmH2O PEEP时)。相应的Bland-Altman分析见图3b, d。如图所示，在PEEP 5 cmH2O时，差异的平均值为0.316 J/min，一致性上限为1.471 J/min，一致性下限为- 0.840 J/min。PEEP为15 cmH2O时，差值均值为−0.840 J/min，一致性上限为0.924 J/min，一致性下限为−2.604 J/min。

通气参数对机械功率的影响

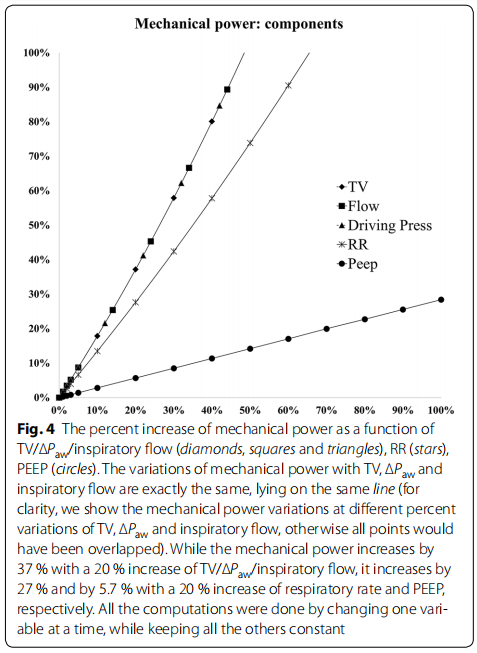
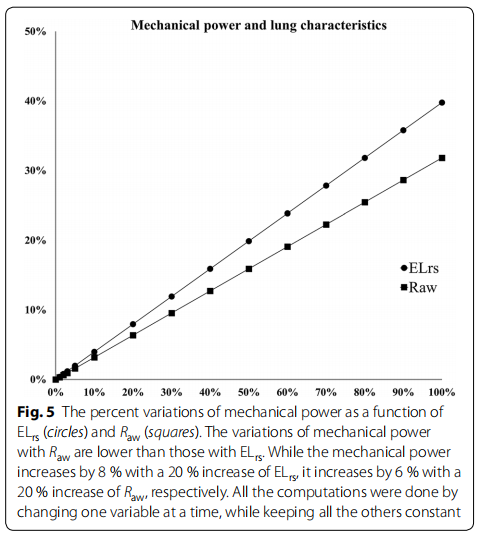
在图4中，从正常状态(ELrs 10 cmH2O/l, Raw 8 cmH2O/l/s)开始，我们展示了机械功率随其中一个组分(TV，∆Paw，吸气流量，RR和PEEP)以10%的步数增加的函数变化，而其他组分保持恒定。如图所示，TV、驱动压和吸气流速相同百分比变化，产生相同的机械功率指数增加(指数= 2)，即使TV加倍(例如，从6 ml/kg增加到12 ml/kg)，产生4倍的机械功率增加。在频率增加相同百分比下，机械功率呈指数增加，但指数为1.4，而PEEP的增加导致机械功率呈线性增加。图5报告了气道阻力和呼吸系统弹性变化对机械功率的影响。

关于呼吸机机械功率不同变量组合的效果可以在专门的计算机程序中看到，可以从以下链接下载: http://www.ains.med.uni_x0002_goettingen.de/de/abteilung-anaesthesiologie/forschung/energy-calculator-software.

讨论

将时间因素与机械功的至少部分成分一起考虑在VILI的发生中显然并不新鲜。我们在这项研究中发现，从经典运动方程(在经典运动方程中加入了PEEP，而忽略了惯性力)导出的“功率方程”得到的结果与通过压力-容积曲线分析得到的实验结果非常相似。对机械功进行数学描述的优势在于，它能够量化不同成分(TV、RR、∆Paw、PEEP、I:E、flow)的相对贡献，并预测它们的变化所产生的影响。

机械功组成

呼吸系统弹性

假定功率方程的第一部分(即与潮气量/驱动压力相关的功率)压力-容积曲线为线性。如果弹性增加接近肺总量，由于过度扩张，计算机计算的能量会低估。相反，如果弹性降低，例如，由于肺复张，计算的能量将高估。然而，必须指出的是，这两种现象(过度扩张和复张)可能同时发生在不同的肺区域，导致总弹性不变。此外，弹性变化(增加或减少)的10 - 20%应对应计算出的机械功率变化(增加或减少)的5 - 10%(见图5)。使用自动化系统测量每个P-V对曲线的导数将避免任何可能的高估或低估。

气道阻力

动力方程的第二部分是与气体运动有关的能量。如图1a所示，在我们的模型中，我们假设在充气过程中阻力和流量都是恒定的。因此，Ppeak - Pplat差立即达到其工作水平，并一直维持到吸气结束。这种假设显然过于简单化了。实际上，在机械通气过程中，随着呼气末肺容积(end-expiratory lung volume, EELV)的增加，气道阻力确实会降低。在正常人群和ARDS患者中，从PEEP 15 cmH2O开始通气时，我们发现计算机计算的机械功均高于实际测量的机械功。在与15 cmH2O PEEP通气相关的Bland - Altman图中，系统计算高估很明显(图2,3d)。此外，在这种情况下，能测量气道阻力和流量的自动化系统将提高计算功率的准确性。

PEEP

功率方程的第三个分量等于在整个吸气阶段克服因PEEP引起的纤维张力所需的能量。在呼吸机进行的呼吸功计算中，不考虑PEEP，因为P-V环从点(0,0)开始，而不考虑PEEP和呼气末肺容量。然而，尽管呼气末正压不增加与通气相关的循环能量负荷，但它的存在增加了传递给呼吸系统的能量负荷，其系数等于呼气末正压x∆V(另见电子附录E-1节)。PEEP的这一作用常被忽视，尽管PEEP增加10 - 20%可使机械功率增加相似程度。

机械功和VILI

VILI起源于向可通气肺实质传递的机械功与可通气肺实质的解剖病理特征相互作用。尽管每一个都是单独研究的，并且可能对机械功的贡献不同，实际上，TV/∆Paw、RR、流速和PEEP都是一个独特物理维度的组成部分。如果对肺实质的机械损伤是机械功率的函数，则可能其成分的不同组合，导致机械功率大于给定阈值，可能产生类似的损伤，正如最近动物实验所表明的那样。显然，由于机械功率受系统电容性特性的影响，因此应以单位肺气量或暴露在通气中的肺组织克数进行标准化。

健康肺

大多数关于健康肺VILI的文献都使用不同的TV和PEEP组合，而为了维持一定的PaCO2范围，RR通常是而设定的。在"正常"频率下，TV大于30 ~ 40 ml/kg或更大时，才会对健康肺造成损伤。若以肺大小作为参照，则对应达到肺总容量(2 ~ 3倍FRC体积)所需的应变。为了了解机械功率与不同物种健康肺的关系，我们认为必须考虑两个因素:第一是肺的尺寸，第二是反映肺实质固有弹性的肺特异性弹性(人类12 cmH2O，猪6 cmH2O和大鼠4 cmH2O)。在平均体重为21 kg，平均FRC为295 ml的健康猪中，我们前瞻性地发现VILI的阈值(通过CT扫描中的水肿评估)为12 J/min，相当于约40 mJ/min/ml。

病变的肺

关于肺大小和特异肺弹性的考虑也适用于急性病变的肺。“婴儿肺”越小，引起损伤所需的机械功率就越低，这部分肺的弹性与正常肺相近。不能通过机械功使"婴儿肺"接近其总容量。然而，病变肺的特点是不同弹性区域之间存在几个界面，这可能使施加的力加倍。事实上，肺的不均一性，即明显的机械力分布不均匀，可能是重力依赖肺VILI发生的主要原因。

研究的局限性

每次呼吸所传递的能量一部分以弹性能量的形式储存起来，一部分通过各种机制散失到肺中。每次呼吸传递的能量一部分以弹性能量的形式储存，一部分通过各种机制消散到肺内。这个分数，由P-V环的滞后面积表示，是一个潜在的有害因素。然而，由于滞后面积占传递能量接近一个恒定的分数(至少在生理潮气量范围内)，为了简单起见，我们参考了最后一个，它可能更容易计算和理解。

能量/功率计算假设肺体积与弹性、阻力之间呈线性关系。如前所述，在较高容量(15 cmH2O PEEP)时，这些线性可能会消失，导致机械功可能被高估/低估。然而，如果机械功的概念被证明是有用的，弹性和阻力可以在P-V回路的每个体积点上自动计算，从而克服线性偏差。

为了了解在功率方程中引入的不同变量的相对权重，我们分别研究它们，同时保持其他变量不变。这种方法显然是有问题的，因为增加潮气量——举个例子——在正常实践中可能与呼吸频率降低、流速变化等有关。然而，我们提供了一个简单的工具来计算任何被认为是合适的变量组合。

必须强调的是，机械动力只是问题的一部分。另一部分是肺的情况。相同的机械功可能会产生不同的影响，这取决于肺的大小、不均一性的存在、应力升高的程度和血管的充盈状态，所有这些因素都导致了所输送的能量的不均匀分布。因此，为了具有临床意义，机械功必须被标准化，至少要与肺容积一致。

结论

机械功分析强调可能具有临床意义的概念。首先，这解释了科学界普遍认可的TV/∆Paw在诱导VILI方面的极端重要性。其次，这可能解释了PEEP的不明确效应。事实上，机械功率随PEEP的增加呈线性增加，可能导致VILI。另一方面，PEEP可以减少依赖肺VILI的原因(肺不均一和交界区开放-塌陷)。最终的效果(积极或消极)将取决于这两种行为中的哪一种起作用以及在哪些患者中起作用。第三，机械功率强调了通常被忽视但潜在相关的呼吸频率的影响，因为当呼吸频率增加时，机械功率呈指数增长。总而言之，把机械功作为一个整体来考虑可能比单独考虑它的各个组成部分提供更好的见解。

E-2 主方程的简化

已知Raw=(Ppeak - Pplat)/F, F=∆V/Tinsp，可将主稿中的式3改写为:

已知ELrs=∆Paw/∆V，则式(I)可改写为:

Paw= Pplat-PEEP。因此:

 

或者：

所以：

E-3 计算肺的机械功

传递给肺部的机械功意味着使用了跨肺压(PL)而不是Pplat和PEEP时的气道压力。PL和Paw之间的关系(Pplat或PEEP)用PL = Paw*(ELL/ELrs)表示，其中ELL为肺弹性。

因此，代入主稿中式6:

PowerL是指输送到肺部的机械功。

根据上述公式，可以计算改变任何变量(潮气量、驱动压、呼吸速率、阻力)对施加于肺部的机械功的影响。